 📚 学びの記録
📚 学びの記録
🔬 炭素同位体解析
 📚 学びの記録
📚 学びの記録  🍳クッキングメモ
🍳クッキングメモ  📡速報キャッチ!
📡速報キャッチ!  📡速報キャッチ!
📡速報キャッチ!  📡速報キャッチ!
📡速報キャッチ! 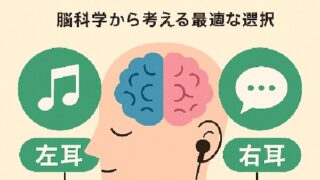 🍀生活のススメ
🍀生活のススメ  🎧 音バズ研究室
🎧 音バズ研究室  🎮ゲーム関係
🎮ゲーム関係  🍀生活のススメ
🍀生活のススメ  🎮ゲーム関係
🎮ゲーム関係  🎮ゲーム関係
🎮ゲーム関係  🍀生活のススメ
🍀生活のススメ  🎮ゲーム関係
🎮ゲーム関係  🚀 発信・成果物
🚀 発信・成果物  🎮ゲーム関係
🎮ゲーム関係  📐 数学ノート
📐 数学ノート  🎮ゲーム関係
🎮ゲーム関係  🍀生活のススメ
🍀生活のススメ  📐 数学ノート
📐 数学ノート  📐 数学ノート
📐 数学ノート  📐 数学ノート
📐 数学ノート  📐 数学ノート
📐 数学ノート  📐 数学ノート
📐 数学ノート